I’ve been playing with fixed points of Haskell functors lately and thought it would be useful to write down some of my thoughts, both to solidify my understanding and for future reference. If it happens to be helpful for someone else, then all the better. I guess I’ll start with Haskell’s category.

Haskell’s Category

The underlying category of Haskell is called Hask. While sometimes we can simply think of it as Set, the category of sets and total functions, Set is, in many cases, an oversimplified approximation of Hask. A much better approximation is a category called CPO⊥, also known as SCPO or CPPO⊥. It is a category where

Objects are pointed cpos. A pointed cpo is a pointed complete partial order (A, ≼) such that it is
- pointed: there exists a bottom element ⊥ ∈ A such that ∀ a ∈ A. ⊥ ≼ a.
- ω-complete: every ascending chain <a> = a0 ≼ a1 ≼ a2 ≼ ... has a least upper bound ⊔<a> ∈ A. A least upper bound (lub) of <a> is an element a such that ∀i. ai ≼ a, and for all a', ∀i. ai ≼ a' implies a ≼ a'.
Arrows are strict continuous functions:
- a strict function f is a function that preserves bottom, i.e., f ⊥ = ⊥.
- a continuous function f between cpos (A, ≼) and (B, ⋞) is a function that is monotonic:
```
a ≼ b  ⟹  f a ⋞ f b
```
  and preserves least upper bounds of ascending chains:
```
f (⊔<a>) = ⊔(<f a>)
```

Let’s look more closely at the objects and the arrows in CPO⊥ and their relationships with Haskell types and functions.

Objects in CPO⊥

Pointed cpos can model Haskell types and functions. The partial order ≼ is an order with respect to degree of definedness or approximation. ⊥ is the least defined value, x ≼ y if x is less defined than y (or x approximates y), and fully defined values are not comparable with one another.

For example, for the natural number data type:

data Nat = Zero | Succ Nat

we have

⊥ ≼ x for all x :: Nat
Succ ⊥ ≼ Succ (Succ ⊥) ≼ Succ (Succ Zero)
Succ (Succ ⊥) ⋠ Succ Zero
Succ Zero ⋠ Succ (Succ Zero)

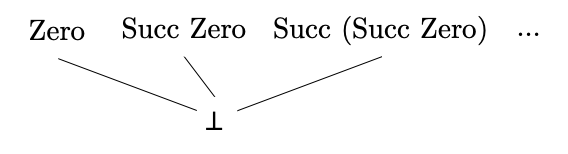
The partial order of the values of Nat can be pictured as

x ≼ y iff there is a path from x to y in the picture going upwards. ∞ is the value Succ (Succ (Succ ...)) with infinitely many Succs, or equivalently,

let inf = Succ inf in inf

∞ must exist because ⊥, Succ ⊥, Succ (Succ ⊥), … is an ascending chain which must have a lub.

For comparison, if we make the Succ constructor strict (i.e., Succ ⊥ = ⊥), then the cpo becomes flat (except for ⊥):

and there is no ∞ value.

For function types like A -> B, the order ≼ is defined as

f ≼ g  ≡  ∀x. f x ≼ g x

In words, f approximates g if and only if every value of f approximates the corresponding value of g.

Arrows in CPO⊥

Continuous Functions

Continuous functions can be used to model computable/implementable functions. As a counter example, the function defined as

f :: Int -> Int
f x = if x is ⊥ then 0 else x

is not monotonic, since ⊥ ≼ 1 but f ⊥ = 0 ⋠ 1 = f 1. Indeed, f is not implementable in Haskell. The only implementable function that maps ⊥ to 0 is const 0, which maps everything to 0.

As another counter example, consider the function

g :: (Int -> Int) -> Int
g f = if f is a total function then 0 else ⊥

g is monotonic but not continuous, because it doesn’t preserve least upper bounds of ascending chains. To see why, consider an ascending chain <f> = f0 ≼ f1 ≼ f2 ≼ ... consisting of functions of type Int -> Int. fi is defined as

fi :: Int -> Int
fi x = if x <= i then x else ⊥

Since fi is not a total function for any i, we have g fi = ⊥ for all i. Thus

⊔(<g f>) = ⊥

On the other hand, ⊔<f> is the identity function, which is total, so

g (⊔<f>) = 0

Therefore g is not continuous. And it is indeed not implementable in Haskell, because to tell whether an arbitrary function is total, one would need to solve the halting problem.

Why Strict?

It seems odd that we are modeling Haskell functions with a category (CPO⊥) that only has strict functions. Are strict continuous functions sufficient to model all Haskell functions, including non-strict ones? The answer is yes: a non-strict function f :: A -> B can be modeled by a strict function of type f' :: Maybe A -> B, defined as

f' ⊥ = ⊥  -- f' is strict
f' Nothing = f ⊥
f' (Just a) = f a

f' is a strict function that is equivalent to f. A number of useful theorems are only applicable to CPO⊥ (and not applicable to CPO, where functions are allowed to be non-strict), such as the existence of initial algebras for locally continuous functors.

Hask is Not CPO or CPO⊥

There are some important differences between Hask and CPO/CPO⊥.

Hask is not even a category, because the existence of seq means undefined . id ≠ undefined. See this Haskell wiki page for more details. The wiki page proposes a solution, which is to define arrow identities extensionally (f and g are considered the same arrow if ∀x. f x = g x), but as Andrej Bauer pointed out, it is not a satisfying solution since f x = g x is not well defined. For now, let’s ignore seq and assume that Hask is indeed a category.
Both CPO and CPO⊥ have categorical products, but Hask does not. In CPO/CPO⊥, the product of two pointed cpos is simply their cartesian product, with (⊥, ⊥) being the bottom element. In Hask, however, the lazy pair, (,), is not a categorical product. This is because (,) is a lifted cartesian product, i.e., ⊥ :: (a, b) and (⊥, ⊥) :: (a, b) are two distinct values, and both x = ⊥ and x = (⊥, ⊥) satisfy
```
fst x = ⊥
snd x = ⊥
```
So we lose the uniqueness of the mediating arrow in the universal property of categorical products.

The strict pair:
```
data P a b = P { fstS :: !a, sndS :: !b }
```
is not a categorical product either, because it is too strict: not only P ⊥ ⊥ = ⊥, but also P x ⊥ = P ⊥ y = ⊥ for all x and y. In order for it to be a categorical product, the universal property mandates that fstS (P x y) = x for all x and y, but fstS (P x ⊥) = ⊥.
Similarly, CPO⊥ has coproducts (although CPO does not), but in Hask, neither Either a b nor its strict counterpart is a categorical coproduct.

To sum up, Hask is messy. It would be much better if it was as nice as Set or even CPO/CPO⊥, and we indeed sometimes reason about Haskell programs as if we have Set or CPO/CPO⊥, but it’s good to be aware of the subtle differences.

Fixed Points of Endofunctors in Hask

Now let’s look at the properties of fixed points for Hask functors, and what are and aren’t fixed points a Haskell functor. This section is mainly example-driven to make it easier to follow by those not super familiar with the topic.

TL;DR

In Haskell, the least fixed point and greatest fixed point of a functor always coincide (however, see the next bullet point).
The universal property of initial algebras in Hask, like CPO, has an additional strictness requirement. So strictly (pardon the unintended pun) speaking, all functors in Hask do not have least fixed points or initial algebras. But we usually implicitly assume the strictness condition, and regard Hask functors as having least fixed points and initial algebras indeed.
Just because the least fixed point and the greatest fixed point of a functor coincide does not mean the functor has a unique fixed point (up to isomorphism).
Mu F is both the least and the greatest fixed point of any Haskell functor F. If F is lazy, this is also the case with Nu F. If F is strict, however, Nu F is not even a fixed point (Mu and Nu are defined in Data.Functor.Foldable).

Fixed Points of NatF

As an example, let’s look at one of the simplest functors, the base functor for natural numbers:

data NatF a = ZeroF | SuccF a

Nat is a Fixed Point of NatF

The lazy natural number type,

data Nat = Zero | Succ Nat

is a fixed point of NatF. The isomorphism between NatF Nat and Nat is witnessed by the following embed and project functions:

embed :: NatF Nat -> Nat
embed ZeroF = Zero
embed (SuccF n) = Succ n

project :: Nat -> NatF Nat
project Zero = ZeroF
project (Succ n) = SuccF n

It is easy to verify that embed . project = id and project . embed = id.

Strict Nat is Not a Fixed Point of NatF

The strict natural number type,

data NatS = ZeroS | SuccS !NatS

is not a fixed point of NatF. Although both NatS and NatF NatS contain a countably infinite number of values, and there always exists a 1-1 mapping between any two countably infinite sets, that mapping is not necessarily continuous, which is a necessary condition for a function to be implementable.

Suppose NatS ≅ NatF NatS, witnessed by a pair of functions embed :: NatF NatS -> NatS and project :: NatS -> NatF NatS. Then, since ⊥ ≼ SuccF ⊥ ≼ SuccF ZeroS, and embed is continuous (hence monotonic), embed must satisfy

embed ⊥ ≼ embed (SuccF ⊥) ≼ embed (SuccF ZeroS)

As shown in a picture before, NatS has a flat structure, and two values x, y :: NatS can only satisfy x ≼ y if x = ⊥. And since embed ⊥, embed (SuccF ⊥) and embed (SuccF ZeroS) are all distinct, it is impossible to satisfy the above ineuqation.

Nat with an Extra Constructor is Not a Fixed Point of NatF

The following NatE type has an additional constructor Extra compared to Nat:

data NatE = ZeroE | SuccE NatE | Extra

NatE is also not a fixed point of NatF, and here’s a proof sketch. Suppose it is, and the isomorphism between NatF NatE and NatE is witnessed by functions embed :: NatF NatE -> NatE and project :: NatE -> NatF NatE.

Since embed is a 1-1 mapping, at least one of embed ZeroF ≠ ZeroE and embed ZeroF ≠ Extra is true. Without loss of generosity, assume embed ZeroF ≠ Extra. Then there must exist some x :: NatE, such that embed (SuccF x) = Extra. By monotonicity, embed must satisfy

embed ⊥ ≼ embed (SuccF ⊥) ≼ Extra

Since the only value strictly less than Extra is ⊥, x can only be ⊥. But this means Extra is strictly less than embed (SuccF ZeroE), which is impossible since Extra is a fully defined value, and no value is strictly greater than Extra.

Canonical Fixed Point and the Strictness Condition

For NatF, and indeed for every Haskell functor, the least fixed point and the greatest fixed point coincide, and it is called the canonical fixed point. And because NatF is lazy, Mu NatF, Nu NatF and Fix NatF are all isomorphic (this is not true for strict functors, which I will explain later).

However, there’s a catch: when we talk about the universal property of initial algebras, there is a strictness condition, namely, if f is a strict function, then cata f is the unique strict function such that the following diagram commutes. This statement is not true if we remove either or both “strict”s.

Here are two examples that demonstrate why the strictness condition is necessary.

Example 1: Let F = Identity whose least fixed point is Void with ⊥ as the sole inhabitant. Let the algebra f be runIdentity :: Identity Int -> Int, which is strict. There is a unique strict arrow cata f that makes the above diagram commute: cata f = const ⊥. However, if we include non-strict arrows, then cata f is no longer unique, since cata f = const x for any x :: Int also makes the diagram commute.

Example 2: Let F = NatF, and let the algebra f be const 0 :: NatF Int -> Int, which is lazy. There is no strict arrow cata f that makes the above diagram commute.

In CPO⊥, since all functions are strict, the strictness requirement is trivially satisfied. Hask is more like CPO which allows non-strict functions, so strictly (again, pardon the pun) speaking, not all functors in Hask have least fixed points or initial algebras, unless we are willing to go loose and implicitly ignore non-strict functions when talking about initial algebras.

On the other hand, greatest fixed points and final coalgebras in Hask do not need the strictness condition. There is, however, no asymmetry between initial algebras and final coalgebras, because the universal property of final coalgebras in fact requires a condition which is the categorical dual of the notion of “strictness”, namely, ⊥ . f = ⊥ (strictness is basically f . ⊥ = ⊥). This is vacuously true for all f.

Fixed Points of NatS (Strict NatF)

UPDATE: Edward Kmett pointed out that NatSF (the strict version of NatF, as defined below) is in fact not a functor since it fails to preserve composition. And that’s why its fixed points behave oddly (e.g., it has fixed points that are not isomorphic to the the least or greatest fixed point, and Nu NatSF is not a fixed point of NatSF). Every lawful Haskell functor F has a unique fixed point (up to isomorphism), and Mu F, Nu F and Fix F all coincide.

Now let’s look at the strict version of NatF, define as

data NatSF a = ZeroSF | SuccSF !a

Strict Nat (NatS) is a Fixed Point of NatSF

The isomorphism between NatSF NatS and NatS is witnessed by

embed :: NatSF NatS -> NatS
embed ZeroSF = ZeroS
embed (SuccSF n) = SuccS n

project :: NatS -> NatSF NatS
project ZeroS = ZeroSF
project (SuccS n) = SuccSF n

In fact NatS is both the least and the greatest fixed point of NatSF, and it is isomorphic to Mu NatSF and Fix NatSF (note that Fix is defined as a newtype, so its constructor is strict). The functions that witness the isomorphisms are left to the readers.

Lazy Nat is Not a Fixed Point of NatSF

The proof that Nat is not a fixed point of NatSF is similar to the proof that NatE is not a fixed point of NatF. Assume Nat ≅ NatSF Nat, witnessed by embed :: NatSF Nat -> Nat and project :: Nat -> NatSF Nat. At least one of project Zero ≠ ZeroS and project Zero ≠ SuccS ZeroS must hold. Suppose project Zero ≠ SuccS ZeroS holds. This means there exists x, such that project (Succ x) = SuccS ZeroS.

If x ≠ ⊥, then both project ⊥ and project (Succ ⊥) must be strictly less than SuccS ZeroS, which is impossible since the only value strictly less than SuccS ZeroS is ⊥.

If x = ⊥, then project (Succ Zero) must be strictly greater than SuccS ZeroS, which is also impossible since no value is strictly greater than SuccS ZeroS.

Strict Nat Remains a Fixed Point of NatSF by Adding Flat Values

Although Nat is not a fixed point of NatSF, interestingly, if we add flat values to NatS, it remains a fixed point of NatSF. Consider the following NatSR type, which adds the set of real numbers to NatS:

data NatSR = ZeroSR | SuccSR !NatSR | Real !Double

NatSR contains an additional flat set of real numbers compared to NatS. NatSR is isomorphic to NatSF NatSR, witnessed by

embed :: NatSF NatSR -> NatSR
embed ZeroFS = ZeroS
embed (SuccFS (Real r)) = Real r
embed (SuccFS n) = SuccS n

project :: NatSR -> NatSF NatSR
project ZeroS = ZeroFS
project (Real r) = SuccSF (Real r)
project (SuccS n) = SuccSF n

It is easy to verify that embed . project = id and project . embed = id.

This begs the question: NatSR is a larger type than NatS since the former has an uncountable number of values while the latter is countable, so why is NatS the greatest fixed point of NatSF?

The answer is that least fixed points and greatest fixed points of functors are not defined in terms of how large the fixed point object is. Rather, they are defined as the carriers of the initial algebra and the final coalgebra, respectively. In the case of NatSF, although NatS is a smaller type than NatSR, it carries both the initial algebra and the final coalgebra, whereas NatSR carries neither. Indeed, there does not exist functions cata and ana of the following types

cata :: (NatSF a -> a) -> NatSR -> a
ana  :: (a -> NatSF a) -> a -> NatSR

such that cata embed = id and ana project = id.

As we can see, the fact that the least fixed point and the greatest fixed point of a functor F coincide does not imply that F has a unique fixed point (up to isomorphism). Rather, we say that F has a canonical fixed point.

Nu F is Not a Fixed Point for Strict Functors

Finally, it is worth mentioning that in Haskell, for functors F whose constructors are strict, not only is Nu F not the greatest fixed point of F, but it is not even a fixed point of F. An example demonstrating this is given below.

{-# LANGUAGE DeriveFunctor #-}

import Data.Functor.Foldable

data NatSF a = ZeroSF | SuccSF !a deriving (Functor)

data Nat = Zero | Succ Nat

nu1 :: Nu NatSF
nu1 = Nu coalg (Succ (Succ undefined))
  where
    coalg Zero = ZeroSF
    coalg (Succ n) = SuccSF n

nu2 :: Nu NatSF
nu2 = embed . project $ nu1

fromNu :: Nu NatSF -> Nat
fromNu (Nu f a) = case f a of
  ZeroSF -> Zero
  SuccSF b -> Succ (fromNu (Nu f b))

nu1 and nu2 above are different, because

fromNu nu1 = Succ ⊥
fromNu nu2 = ⊥

which means embed . project ≠ id. Therefore Nu NatSF is not a fixed point of NatSF.

Nu F for strict F is useful for encoding infinite values. For example, neither Mu NatSF nor Fix NatSF includes the ∞ value, but Nu NatSF does:

inf :: Nu NatSF
inf = Nu SuccSF ()

But if you need the least or greatest fixed point, use Mu or Fix.

Acknowledgement

A number of discussions with Greg Pfeil have helped clarify some of my confusions.

Ziyang Liu's Haskell Blog

Fixed Points and Non-Fixed Points of Haskell Functors